Mengungkap Rahasia Angka: Faktorisasi, Petualangan Baru di Dunia Matematika Kelas 4

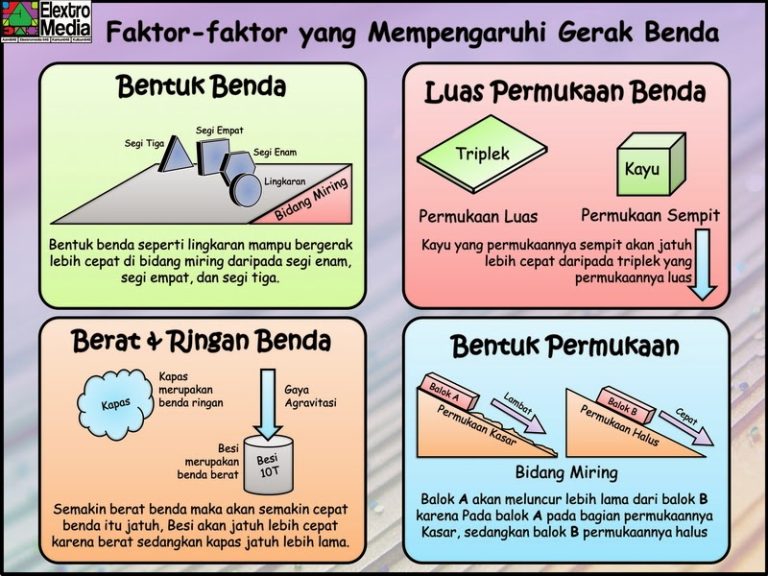
Halo, para matematikawan cilik! Pernahkah kalian merasa angka-angka itu seperti puzzle yang menunggu untuk dipecahkan? Di kelas 4 ini, kita akan memulai petualangan seru untuk mengungkap salah satu rahasia tersembunyi di balik angka, yaitu faktorisasi. Jangan khawatir, ini bukan tentang menyembunyikan sesuatu, justru sebaliknya, faktorisasi adalah tentang memecah angka menjadi bagian-bagian kecil yang membangunnya. Mari kita selami dunia faktorisasi bersama!

Apa Itu Faktorisasi? Bayangkan Seperti Membongkar Mainan!

Coba bayangkan kalian punya sebuah mainan balok yang terdiri dari banyak balok kecil yang tersusun rapi. Faktorisasi itu mirip seperti membongkar mainan tersebut, tapi bukan sembarang membongkar. Kita membongkar angka menjadi perkalian dari angka-angka yang lebih kecil.

Secara sederhana, faktorisasi sebuah bilangan adalah cara menuliskan bilangan tersebut sebagai hasil perkalian dari dua bilangan bulat atau lebih. Angka-angka yang dikalikan ini disebut faktor.

Mari kita ambil contoh yang mudah. Angka 6. Bisakah kita menemukan dua angka yang jika dikalikan hasilnya adalah 6? Ya, tentu saja!

• 1 dikalikan 6 sama dengan 6. (1 x 6 = 6)
• 2 dikalikan 3 sama dengan 6. (2 x 3 = 6)

Jadi, angka-angka 1, 2, 3, dan 6 adalah faktor dari angka 6. Ketika kita menulis 6 sebagai 1 x 6 atau 2 x 3, kita sedang melakukan faktorisasi dari angka 6.

Mengapa Kita Perlu Belajar Faktorisasi? Ini Seperti Punya Alat Super!

Mungkin ada yang bertanya, "Untuk apa kita repot-repot memecah angka?" Faktorisasi itu punya banyak kegunaan, lho! Di kelas 4 ini, faktorisasi akan menjadi alat bantu kita untuk memahami konsep matematika lainnya dengan lebih baik. Beberapa manfaatnya antara lain:

1. Memahami Bilangan Prima dan Komposit: Nanti kita akan belajar tentang bilangan spesial yang hanya punya dua faktor, yaitu 1 dan dirinya sendiri (bilangan prima). Faktorisasi membantu kita mengidentifikasi bilangan prima.
2. Menyederhanakan Pecahan: Jika kalian nanti bertemu pecahan yang rumit, faktorisasi akan menjadi kunci untuk menyederhanakannya.
3. Menemukan Kelipatan Persekutuan Terkecil (KPK) dan Faktor Persekutuan Terbesar (FPB): Ini adalah topik penting lainnya yang akan kalian pelajari, dan faktorisasi adalah salah satu cara untuk menemukannya.
4. Memecahkan Soal Cerita yang Lebih Kompleks: Banyak soal cerita yang melibatkan pembagian atau perkalian yang bisa diselesaikan lebih mudah dengan pemahaman faktorisasi.

Mengenal Faktor: Teman-Teman Angka Kita

Setiap angka punya "teman-teman" yang jika dikalikan akan menghasilkan angka itu sendiri. Teman-teman inilah yang kita sebut faktor.

Cara Mencari Faktor:

Cara termudah untuk mencari faktor dari sebuah bilangan adalah dengan mencoba membaginya dengan bilangan lain, mulai dari angka 1.

• Contoh: Mencari faktor dari 12

  • Apakah 12 bisa dibagi 1 tanpa sisa? Ya. 12 : 1 = 12. Jadi, 1 dan 12 adalah faktor dari 12. (1 x 12 = 12)
  • Apakah 12 bisa dibagi 2 tanpa sisa? Ya. 12 : 2 = 6. Jadi, 2 dan 6 adalah faktor dari 12. (2 x 6 = 12)
  • Apakah 12 bisa dibagi 3 tanpa sisa? Ya. 12 : 3 = 4. Jadi, 3 dan 4 adalah faktor dari 12. (3 x 4 = 12)
  • Apakah 12 bisa dibagi 4 tanpa sisa? Ya, tapi 4 sudah kita temukan pasangannya yaitu 3. Kita bisa berhenti di sini karena jika kita lanjutkan, kita akan menemukan pasangan faktor yang sudah ada.

  Jadi, faktor-faktor dari 12 adalah 1, 2, 3, 4, 6, dan 12.

Latihan Mencari Faktor:

Mari kita coba mencari faktor dari beberapa angka:

1. Angka 8:

   • 1 x 8 = 8. Faktornya adalah 1 dan 8.
   • 2 x 4 = 8. Faktornya adalah 2 dan 4.
   • Faktor dari 8 adalah: 1, 2, 4, 8.

2. Angka 15:

   • 1 x 15 = 15. Faktornya adalah 1 dan 15.
   • 3 x 5 = 15. Faktornya adalah 3 dan 5.
   • Faktor dari 15 adalah: 1, 3, 5, 15.

3. Angka 20:

   • 1 x 20 = 20. Faktornya adalah 1 dan 20.
   • 2 x 10 = 20. Faktornya adalah 2 dan 10.
   • 4 x 5 = 20. Faktornya adalah 4 dan 5.
   • Faktor dari 20 adalah: 1, 2, 4, 5, 10, 20.

Faktorisasi Prima: Memecah Sampai Paling Kecil!

Selain memecah angka menjadi perkalian dua bilangan, kita juga bisa memecahnya terus menerus sampai semua faktornya adalah bilangan prima. Bilangan prima adalah bilangan yang hanya bisa dibagi oleh 1 dan dirinya sendiri. Contoh bilangan prima adalah 2, 3, 5, 7, 11, 13, dan seterusnya.

Proses memecah sebuah bilangan menjadi perkalian bilangan-bilangan prima disebut faktorisasi prima.

Cara Melakukan Faktorisasi Prima:

Ada dua cara umum untuk melakukan faktorisasi prima:

Metode Pohon Faktor:

Ini adalah metode yang paling visual dan menyenangkan. Bayangkan kita membuat pohon yang cabangnya memunculkan faktor-faktornya.

• Contoh: Faktorisasi prima dari 24

  1. Mulai dengan angka 24 di bagian atas.
  2. Cari dua bilangan yang jika dikalikan hasilnya 24. Misalnya, 4 x 6. Gambarlah dua cabang dari 24 menuju 4 dan 6.

           24
          /  
         4    6

  3. Sekarang, periksa apakah 4 dan 6 adalah bilangan prima.
     • 4 bukan bilangan prima (bisa dibagi 2). Pecah lagi 4 menjadi 2 x 2.
     • 6 bukan bilangan prima (bisa dibagi 2 dan 3). Pecah lagi 6 menjadi 2 x 3.

         24
        /  
       4    6
       /   / 
       2  2 2   3

  4. Perhatikan bilangan-bilangan di ujung cabang pohon: 2, 2, 2, dan 3. Apakah semuanya bilangan prima? Ya!
  5. Jadi, faktorisasi prima dari 24 adalah 2 x 2 x 2 x 3. Kita bisa menuliskannya dalam bentuk perpangkatan sebagai 2³ x 3.

Metode Pembagian Berulang:

Cara ini lebih ringkas dan cocok jika kita sudah hafal perkalian dan pembagian.

• Contoh: Faktorisasi prima dari 36

  1. Mulai dengan angka 36.
  2. Bagi 36 dengan bilangan prima terkecil yang bisa membaginya tanpa sisa. Bilangan prima terkecil adalah 2.
     36 : 2 = 18. Tulis 2 di sebelah kiri.

     2 | 36
       ----
         18

  3. Sekarang, ambil hasil pembagiannya, yaitu 18. Bagi lagi dengan bilangan prima terkecil yang bisa membaginya. 18 masih bisa dibagi 2.
     18 : 2 = 9. Tulis 2 di sebelah kiri.

     2 | 36
       ----
     2 | 18
       ----
          9

  4. Sekarang, ambil hasil pembagiannya, yaitu 9. Apakah 9 bisa dibagi 2? Tidak. Coba bilangan prima selanjutnya, yaitu 3.
     9 : 3 = 3. Tulis 3 di sebelah kiri.

     2 | 36
       ----
     2 | 18
       ----
     3 |  9
       ----
          3

  5. Sekarang, ambil hasil pembagiannya, yaitu 3. Apakah 3 bisa dibagi 3? Ya.
     3 : 3 = 1. Tulis 3 di sebelah kiri.

     2 | 36
       ----
     2 | 18
       ----
     3 |  9
       ----
     3 |  3
       ----
          1

  6. Kita berhenti ketika hasil pembagiannya adalah 1.
  7. Angka-angka di sebelah kiri adalah faktor prima dari 36: 2, 2, 3, 3.
  8. Jadi, faktorisasi prima dari 36 adalah 2 x 2 x 3 x 3. Dalam bentuk perpangkatan, ini adalah 2² x 3².

Penting untuk Diingat:

• Selalu mulai pembagian dengan bilangan prima terkecil (2, 3, 5, 7, dst.).
• Lanjutkan membagi sampai hasil akhirnya adalah 1.

Contoh Soal Latihan Faktorisasi Prima:

Mari kita coba memfaktorkan bilangan-bilangan berikut menjadi faktor primanya:

1. Faktorisasi prima dari 18:

   • Menggunakan metode pohon: 18 -> 2 x 9 -> 2 x 3 x 3. Faktor primanya adalah 2, 3, 3. (2 x 3² )

   • Menggunakan pembagian berulang:
     2 | 18

     3 | 9

     3 | 3

      1

     Faktor primanya adalah 2, 3, 3. (2 x 3²)

2. Faktorisasi prima dari 30:

   • Menggunakan metode pohon: 30 -> 2 x 15 -> 2 x 3 x 5. Faktor primanya adalah 2, 3, 5. (2 x 3 x 5)

   • Menggunakan pembagian berulang:
     2 | 30

     3 | 15

     5 | 5

      1

     Faktor primanya adalah 2, 3, 5. (2 x 3 x 5)

3. Faktorisasi prima dari 42:

   • Menggunakan metode pohon: 42 -> 2 x 21 -> 2 x 3 x 7. Faktor primanya adalah 2, 3, 7. (2 x 3 x 7)

   • Menggunakan pembagian berulang:
     2 | 42

     3 | 21

     7 | 7

      1

     Faktor primanya adalah 2, 3, 7. (2 x 3 x 7)

Soal-Soal Latihan untuk Mengasah Kemampuan:

Sekarang, saatnya kalian mencoba sendiri! Cobalah kerjakan soal-soal berikut:

Bagian 1: Mencari Faktor

Temukan semua faktor dari bilangan-bilangan berikut:

1. 10
2. 16
3. 25
4. 28
5. 32

Bagian 2: Faktorisasi Prima

Temukan faktorisasi prima dari bilangan-bilangan berikut menggunakan metode pohon atau pembagian berulang:

1. 14
2. 20
3. 27
4. 40
5. 50
6. 60
7. 75
8. 100

Petunjuk Tambahan:

• Jika kalian kesulitan mencari faktor awal untuk metode pohon, ingatlah ciri-ciri bilangan yang habis dibagi 2, 3, 5.
  • Habis dibagi 2 jika angka terakhirnya genap (0, 2, 4, 6, 8).
  • Habis dibagi 3 jika jumlah angka-angkanya habis dibagi 3 (contoh: 18 -> 1+8=9, 9 habis dibagi 3).
  • Habis dibagi 5 jika angka terakhirnya 0 atau 5.
• Untuk metode pembagian berulang, selalu mulai dari pembagian dengan angka 2, lalu 3, lalu 5, dan seterusnya bilangan prima.

Kesimpulan: Faktorisasi, Kunci Membuka Dunia Angka

Faktorisasi memang terdengar seperti sebuah tugas yang rumit, namun dengan latihan dan pemahaman yang benar, kalian akan melihat bahwa ini adalah sebuah petualangan yang menarik. Memahami bagaimana sebuah angka tersusun dari perkalian faktor-faktornya akan memberikan kalian wawasan yang lebih dalam tentang dunia matematika.

Ingatlah, setiap bilangan memiliki "sidik jari" unik yang terdiri dari faktor-faktor primanya. Dengan menguasai faktorisasi, kalian sedang membangun fondasi yang kuat untuk menghadapi berbagai tantangan matematika yang lebih seru di masa depan. Teruslah berlatih, jangan ragu untuk bertanya, dan nikmati proses belajar kalian! Selamat memecahkan kode angka!