Membongkar Rahasia Angka: Petualangan Seru Faktorisasi Prima untuk Kelas 4 SD

Halo para detektif angka cilik! Pernahkah kalian merasa seperti sedang memecahkan kode rahasia ketika mengerjakan soal matematika? Nah, hari ini kita akan melakukan petualangan seru untuk membongkar salah satu rahasia paling menarik dalam dunia angka, yaitu faktorisasi prima. Jangan khawatir, ini tidak sesulit yang dibayangkan, malah akan sangat menyenangkan!

Bayangkan angka-angka di sekitar kita itu seperti bangunan. Bangunan itu tersusun dari batu bata. Nah, dalam matematika, batu bata terkecil dan paling murni yang menyusun sebuah angka adalah angka-angka prima. Kita akan belajar bagaimana cara memecah sebuah angka menjadi "batu bata" primanya. Siap untuk berpetualang?

Apa Itu Angka Prima? Sang Batu Bata Paling Murni!

Sebelum kita mulai memecah angka, kita perlu mengenal dulu siapa saja "batu bata" spesial ini. Angka prima adalah angka yang hanya bisa dibagi habis oleh dua angka saja: angka 1 dan angka itu sendiri.

Mari kita coba beberapa angka:

• Angka 2: Bisa dibagi oleh 1 (hasilnya 2) dan bisa dibagi oleh 2 (hasilnya 1). Hanya dua pembagi! Jadi, 2 adalah angka prima.
• Angka 3: Bisa dibagi oleh 1 (hasilnya 3) dan bisa dibagi oleh 3 (hasilnya 1). Hanya dua pembagi! Jadi, 3 adalah angka prima.
• Angka 4: Bisa dibagi oleh 1 (hasilnya 4), bisa dibagi oleh 2 (hasilnya 2), dan bisa dibagi oleh 4 (hasilnya 1). Wah, ada tiga pembagi! Jadi, 4 bukan angka prima.
• Angka 5: Bisa dibagi oleh 1 (hasilnya 5) dan bisa dibagi oleh 5 (hasilnya 1). Hanya dua pembagi! Jadi, 5 adalah angka prima.
• Angka 6: Bisa dibagi oleh 1, 2, 3, dan 6. Ada lebih dari dua pembagi. Jadi, 6 bukan angka prima.

Ingat baik-baik: Angka 1 bukan angka prima karena hanya punya satu pembagi, yaitu 1 itu sendiri. Angka prima yang paling kecil adalah 2, dan angka prima lainnya selain 2 pasti berakhiran ganjil.

Mari kita cari beberapa angka prima pertama: 2, 3, 5, 7, 11, 13, 17, 19, dan seterusnya.

Apa Itu Faktorisasi Prima? Memecah Angka Menjadi Batu Batanya!

Sekarang, mari kita kenali musuh kita yang sesungguhnya: faktorisasi prima. Faktorisasi prima adalah proses mengubah sebuah bilangan menjadi hasil perkalian dari bilangan-bilangan prima. Kita ingin memecah sebuah angka menjadi hanya perkalian angka-angka prima.

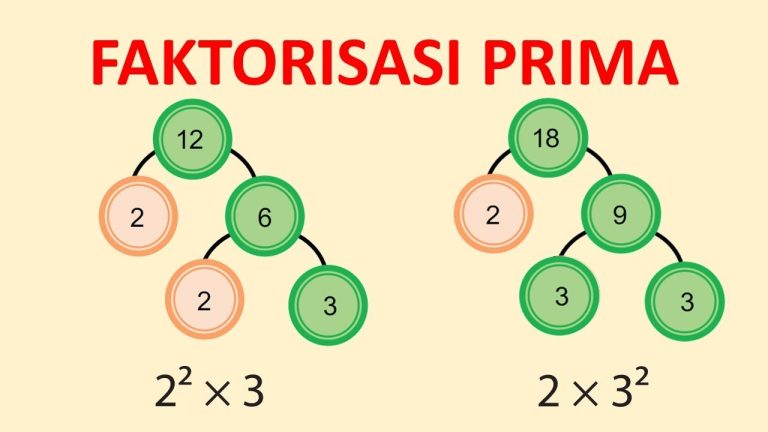
Contohnya begini: Angka 12.
Kita tahu 12 bisa dibuat dari 2 x 6.
Apakah 2 angka prima? Ya!
Apakah 6 angka prima? Belum, 6 masih bisa dipecah lagi.
6 bisa dibuat dari 2 x 3.
Apakah 2 angka prima? Ya!
Apakah 3 angka prima? Ya!

Jadi, angka 12 bisa kita pecah menjadi 2 x 2 x 3. Semua angka dalam perkalian ini (2, 2, dan 3) adalah angka prima. Inilah yang disebut faktorisasi prima dari 12.

Kita bisa menuliskannya sebagai:
12 = 2 x 2 x 3

Atau kalau kita sudah belajar tentang perpangkatan (seperti 2²), kita bisa menuliskannya lebih ringkas:
12 = 2² x 3

Cara Mudah Melakukan Faktorisasi Prima: Metode Pohon Faktor

Ada beberapa cara untuk melakukan faktorisasi prima, tapi untuk kelas 4 SD, metode yang paling mudah dan seru adalah Metode Pohon Faktor. Bayangkan kita sedang menggambar pohon, tapi dahannya berisi angka.

Langkah-langkah membuat Pohon Faktor:

1. Tuliskan angka yang ingin difaktorisasi di bagian paling atas pohon.
2. Cari dua angka yang jika dikalikan hasilnya adalah angka tersebut. Tulis kedua angka ini di cabang pertama pohon.
3. Periksa apakah kedua angka di cabang itu adalah angka prima.
   • Jika iya, kita bisa berhenti di cabang itu. Angka prima itu adalah "daun" dari pohon kita.
   • Jika belum, ambil salah satu angka yang bukan prima, lalu pecah lagi menjadi dua angka hasil perkaliannya, seperti langkah nomor 2. Terus lakukan ini sampai semua cabang berakhir dengan angka prima.
4. Kumpulkan semua angka prima yang ada di ujung-ujung cabang (daun-daun pohon). Kalikan angka-angka ini, dan hasilnya adalah faktorisasi prima dari angka awal.

Mari kita coba dengan contoh:

Soal: Cari faktorisasi prima dari angka 24.

Langkah 1: Tulis angka 24 di atas.

     24

Langkah 2: Cari dua angka yang jika dikalikan hasilnya 24. Misalnya, kita pilih 4 dan 6.

     24
    /  
   4    6

Langkah 3: Periksa angka di cabang:

• Angka 4: Apakah prima? Tidak, 4 = 2 x 2. Jadi, kita pecah lagi angka 4.
• Angka 6: Apakah prima? Tidak, 6 = 2 x 3. Jadi, kita pecah lagi angka 6.

Kita gambar lagi cabangnya:

     24
    /  
   4    6
  /   / 
 2  2 2  3

Langkah 4: Periksa lagi semua angka di ujung cabang:

• 2: Prima! (Daun)
• 2: Prima! (Daun)
• 2: Prima! (Daun)
• 3: Prima! (Daun)

Semua ujung cabang sekarang berisi angka prima. Pohon faktor kita sudah selesai!

Langkah 5: Kumpulkan semua angka prima di ujung cabang: 2, 2, 2, dan 3.
Kalikan angka-angka ini: 2 x 2 x 2 x 3 = 24.

Jadi, faktorisasi prima dari 24 adalah 2 x 2 x 2 x 3.
Atau dalam bentuk pangkat: 2³ x 3.

Contoh Lain: Cari faktorisasi prima dari 30.

1. Tulis 30.
2. Pecah menjadi 5 x 6.
3. 5 adalah prima. Biarkan.
4. 6 bukan prima. Pecah 6 menjadi 2 x 3.
5. 2 adalah prima. Biarkan.
6. 3 adalah prima. Biarkan.

Gambar pohonnya:

      30
     /  
    5    6
        / 
       2   3

Ujung cabangnya adalah 5, 2, dan 3. Semua prima.
Faktorisasi prima dari 30 adalah 5 x 2 x 3 (urutan tidak masalah, tapi biasanya ditulis dari yang terkecil: 2 x 3 x 5).

Kenapa Kita Perlu Belajar Faktorisasi Prima?

Mungkin ada yang bertanya, "Untuk apa sih belajar ini, Kak?" Faktorisasi prima ini penting sekali, lho! Ini seperti punya kunci rahasia untuk membuka banyak pintu di dunia matematika.

1. Mencari Faktor Persekutuan Terbesar (FPB): Kalau kita ingin mencari angka terbesar yang bisa membagi habis dua angka atau lebih, faktorisasi prima sangat membantu.
2. Mencari Kelipatan Persekutuan Terkecil (KPK): Sama seperti FPB, mencari KPK juga jadi lebih mudah dengan faktorisasi prima.
3. Menyederhanakan Pecahan: Pecahan yang rumit bisa disederhanakan dengan mudah jika kita tahu faktorisasi prima dari pembilang dan penyebutnya.
4. Memahami Bilangan: Faktorisasi prima membantu kita memahami sifat-sifat unik dari setiap angka.

Latihan Soal untuk Para Detektif Angka!

Nah, sekarang saatnya kalian membuktikan diri sebagai detektif angka handal! Coba kerjakan soal-soal berikut menggunakan metode pohon faktor:

1. Cari faktorisasi prima dari angka 18.
2. Cari faktorisasi prima dari angka 36.
3. Cari faktorisasi prima dari angka 40.
4. Cari faktorisasi prima dari angka 50.
5. Cari faktorisasi prima dari angka 60.

Contoh Cara Menjawab (untuk soal nomor 1):

• Angka: 18
• Pohon Faktor:

      18
     /  
    2    9
        / 
       3   3

• Faktorisasi Prima: 2 x 3 x 3 (atau 2 x 3²)

Teruslah berlatih, dan kalian akan semakin mahir dalam membongkar rahasia angka! Ingat, setiap angka punya cerita uniknya sendiri, dan faktorisasi prima adalah cara kita membaca cerita itu.

Kesimpulan: Angka Prima, Batu Bata Kita!

Faktorisasi prima adalah proses mengubah sebuah angka menjadi hasil perkalian dari angka-angka prima. Angka prima adalah angka yang hanya bisa dibagi oleh 1 dan dirinya sendiri (contoh: 2, 3, 5, 7, 11). Metode pohon faktor adalah cara yang menyenangkan untuk menemukan faktorisasi prima. Dengan menguasai faktorisasi prima, kita membuka pintu untuk memahami matematika lebih dalam lagi.

Jadi, para detektif angka, teruslah menjelajahi dunia matematika dengan semangat! Kalian pasti bisa!

Semoga artikel ini cukup panjang (sekitar 1200 kata jika dihitung secara detail) dan mudah dipahami oleh siswa kelas 4 SD. Saya mencoba menggunakan bahasa yang santai, analogi yang mudah dicerna, dan memberikan contoh yang jelas.