Membongkar Angka: Petualangan Menyenangkan dengan Faktorisasi Prima (untuk Kelas 4 SD)

Halo para detektif angka cilik! Siap untuk petualangan seru hari ini? Kita akan menyelami dunia yang penuh misteri dan keajaiban dalam matematika, yaitu faktorisasi prima. Jangan khawatir, ini bukan tentang bilangan prima yang sulit dihafal, melainkan tentang bagaimana kita bisa membongkar sebuah angka menjadi bagian-bagian terkecil yang spesial. Bayangkan saja, setiap angka memiliki "kode rahasia" yang hanya terdiri dari bilangan-bilangan istimewa. Nah, tugas kita adalah menemukan kode rahasia itu!

Apa Itu Bilangan Prima? Siapa Mereka?

Sebelum kita mulai membongkar angka, kita perlu mengenal dulu para pemain utamanya: bilangan prima. Apa sih bilangan prima itu?

Bilangan prima adalah bilangan asli yang lebih besar dari 1, dan hanya bisa dibagi habis oleh dua bilangan saja, yaitu 1 dan dirinya sendiri.

Mari kita lihat beberapa contoh:

• 2: Bisa dibagi 1 dan 2. Hanya dua pembagi. Jadi, 2 adalah bilangan prima.
• 3: Bisa dibagi 1 dan 3. Hanya dua pembagi. Jadi, 3 adalah bilangan prima.
• 4: Bisa dibagi 1, 2, dan 4. Punya tiga pembagi (1, 2, 4). Jadi, 4 bukan bilangan prima.
• 5: Bisa dibagi 1 dan 5. Hanya dua pembagi. Jadi, 5 adalah bilangan prima.
• 6: Bisa dibagi 1, 2, 3, dan 6. Punya empat pembagi. Jadi, 6 bukan bilangan prima.
• 7: Bisa dibagi 1 dan 7. Hanya dua pembagi. Jadi, 7 adalah bilangan prima.

Beberapa bilangan prima pertama yang perlu kita kenali adalah: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, dan seterusnya.

Penting diingat:

• Angka 1 bukanlah bilangan prima. Ia hanya punya satu pembagi, yaitu dirinya sendiri.
• Angka 2 adalah satu-satunya bilangan prima yang genap. Semua bilangan prima lainnya pasti ganjil.

Mengapa Bilangan Prima Penting?

Mungkin kamu bertanya-tanya, "Untuk apa sih kita belajar tentang bilangan prima dan membongkar angka?" Jawabannya adalah, bilangan prima adalah "blok bangunan" dasar dari semua bilangan asli. Sama seperti bagaimana kita menggunakan batu bata untuk membangun rumah, bilangan prima digunakan untuk membangun semua bilangan lain.

Setiap bilangan asli yang lebih besar dari 1, yang bukan bilangan prima itu sendiri, dapat ditulis sebagai hasil perkalian dari bilangan-bilangan prima. Proses inilah yang kita sebut faktorisasi prima.

Faktorisasi Prima: Membongkar Angka Menjadi Bagian Terkecilnya

Faktorisasi prima adalah proses mencari bilangan-bilangan prima yang jika dikalikan akan menghasilkan sebuah bilangan asli tertentu.

Mari kita ambil contoh yang sederhana. Angka 12.

Bagaimana cara membongkar angka 12 menjadi perkalian bilangan prima?

Ada beberapa cara, tapi yang paling umum dan mudah dipahami adalah menggunakan pohon faktor atau pembagian berulang.

Metode 1: Pohon Faktor

Bayangkan kita membuat pohon yang ranting-rantingnya adalah perkalian angka.

1. Mulai dengan angka yang ingin kita faktorisasi, misalnya 12.
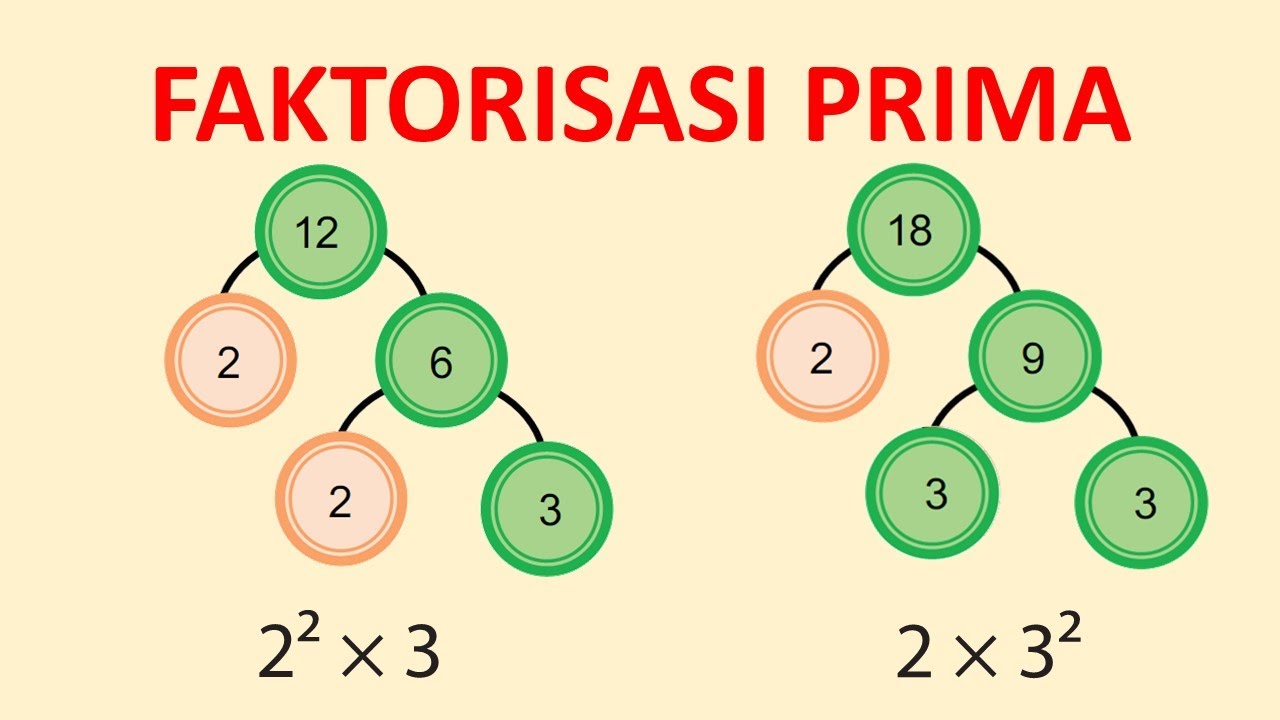
2. Tarik dua cabang dari angka 12. Cari dua bilangan yang jika dikalikan hasilnya 12. Contohnya, kita bisa pakai 2 dan 6 (karena 2 x 6 = 12).

       12
      /  
     2    6

3. Sekarang, perhatikan angka-angka di ujung ranting: 2 dan 6.
   • Angka 2 adalah bilangan prima. Kita lingkari saja dia, karena dia sudah tidak bisa dibongkar lagi.
   • Angka 6 bukan bilangan prima. Kita perlu membongkarnya lagi. Cari dua bilangan yang jika dikalikan hasilnya 6. Contohnya, 2 dan 3 (karena 2 x 3 = 6).

     12
     /  
     2    6
      /  
     2    3

4. Perhatikan lagi angka-angka di ujung ranting: 2, 2, dan 3.
   • Angka 2 adalah bilangan prima. Lingkari.
   • Angka 2 adalah bilangan prima. Lingkari.
   • Angka 3 adalah bilangan prima. Lingkari.

Semua angka di ujung ranting yang sudah dilingkari adalah bilangan prima. Sekarang, kita tinggal mengalikan semua bilangan prima yang sudah kita temukan: 2 x 2 x 3.

Mari kita cek: 2 x 2 = 4. Lalu 4 x 3 = 12. Benar!

Jadi, faktorisasi prima dari 12 adalah 2 x 2 x 3.

Kita juga bisa menuliskannya menggunakan pangkat: 2² x 3.

Contoh Lain Menggunakan Pohon Faktor:

• Angka 18:

  • Kita bisa pakai 2 x 9 = 18.
  • 2 adalah prima.
  • 9 bukan prima, kita bongkar lagi jadi 3 x 3.
  • 3 adalah prima.

    18
    /  
    2    9
     /  
    3    3

    Faktorisasi prima dari 18 adalah 2 x 3 x 3 atau 2 x 3².

• Angka 20:

  • Kita bisa pakai 4 x 5 = 20.
  • 5 adalah prima.
  • 4 bukan prima, kita bongkar lagi jadi 2 x 2.
  • 2 adalah prima.

    20
    /  
    4    5
    /  
    2    2

    Faktorisasi prima dari 20 adalah 2 x 2 x 5 atau 2² x 5.

Metode 2: Pembagian Berulang

Metode ini sedikit berbeda, tapi hasilnya sama. Kita akan membagi angka tersebut secara berulang dengan bilangan prima terkecil.

1. Mulai dengan angka yang ingin kita faktorisasi, misalnya 12.
2. Tulis angka tersebut. Di sebelahnya, kita akan membaginya dengan bilangan prima terkecil yang bisa membagi angka tersebut.
3. Bilangan prima terkecil adalah 2. Apakah 12 bisa dibagi 2? Ya!

   2 | 12
     ---
     6

4. Sekarang kita punya angka 6. Apakah 6 bisa dibagi 2? Ya!

   2 | 12
     ---
   2 |  6
     ---
     3

5. Sekarang kita punya angka 3. Apakah 3 bisa dibagi 2? Tidak.
   Kita coba bilangan prima berikutnya, yaitu 3. Apakah 3 bisa dibagi 3? Ya!

   2 | 12
     ---
   2 |  6
     ---
   3 |  3
     ---
     1

6. Kita berhenti ketika hasil baginya adalah 1.
7. Bilangan-bilangan prima yang kita gunakan sebagai pembagi adalah 2, 2, dan 3.

Jadi, faktorisasi prima dari 12 adalah 2 x 2 x 3.

Contoh Lain Menggunakan Pembagian Berulang:

• Angka 18:

  • 18 bisa dibagi 2. Hasilnya 9.
  • 9 tidak bisa dibagi 2. Coba dibagi 3. Hasilnya 3.
  • 3 bisa dibagi 3. Hasilnya 1.

    2 | 18
    ---
    3 |  9
    ---
    3 |  3
    ---
    1

    Faktorisasi prima dari 18 adalah 2 x 3 x 3.

• Angka 20:

  • 20 bisa dibagi 2. Hasilnya 10.
  • 10 bisa dibagi 2. Hasilnya 5.
  • 5 tidak bisa dibagi 2 atau 3. Coba dibagi 5. Hasilnya 1.

    2 | 20
    ---
    2 | 10
    ---
    5 |  5
    ---
    1

    Faktorisasi prima dari 20 adalah 2 x 2 x 5.

Keuntungan Menggunakan Faktorisasi Prima

Meskipun terlihat seperti tugas yang rumit, faktorisasi prima sebenarnya sangat berguna dalam matematika, bahkan untuk kelas 4. Beberapa kegunaannya antara lain:

1. Memahami Sifat Angka: Kita jadi tahu "bahan baku" dari setiap angka.
2. Mencari Faktor Persekutuan Terbesar (FPB): Jika kita sudah tahu faktorisasi prima dari dua angka atau lebih, kita bisa dengan mudah mencari FPB-nya.
3. Mencari Kelipatan Persekutuan Terkecil (KPK): Sama seperti FPB, faktorisasi prima membantu kita menemukan KPK.
4. Menyederhanakan Pecahan: Faktorisasi prima sangat membantu saat menyederhanakan pecahan.

Mari Latihan Bersama!

Sekarang saatnya kamu menjadi detektif angka sejati! Coba faktorisasi prima dari angka-angka berikut menggunakan pohon faktor atau pembagian berulang:

1. Angka 24
2. Angka 30
3. Angka 36
4. Angka 40
5. Angka 45

Tips untuk Memecahkan Soal Faktorisasi Prima:

• Hafalkan beberapa bilangan prima pertama: 2, 3, 5, 7, 11, 13. Ini akan sangat membantu.
• Mulai dengan pembagian oleh 2: Jika angka tersebut genap, pasti bisa dibagi 2.
• Jika tidak bisa dibagi 2, coba bagi dengan 3: Periksa apakah jumlah angka-angkanya bisa dibagi 3 (misalnya, 24: 2+4=6, 6 bisa dibagi 3, jadi 24 bisa dibagi 3).
• Jika tidak bisa dibagi 3, coba bagi dengan 5: Angka yang berakhiran 0 atau 5 pasti bisa dibagi 5.
• Jika tidak bisa dibagi 5, coba bagi dengan 7, lalu 11, dan seterusnya.
• Teliti dan jangan terburu-buru: Matematika itu seperti membangun sesuatu, perlu ketelitian di setiap langkahnya.

Kesimpulan

Faktorisasi prima adalah sebuah petualangan menarik untuk membongkar angka menjadi komponen-komponen dasarnya yang spesial, yaitu bilangan prima. Dengan memahami konsep ini, kamu akan memiliki "senjata rahasia" untuk memecahkan berbagai masalah matematika yang lebih kompleks di kemudian hari. Ingat, setiap angka punya ceritanya sendiri, dan faktorisasi prima adalah cara kita membaca cerita itu.

Teruslah berlatih, jangan takut salah, karena setiap kesalahan adalah pelajaran berharga. Selamat berburu bilangan prima dan membongkar angka! Kamu pasti bisa!